20. Convergence of Positive Series

g. Approximating the Series

Once we know that a positive series \(\displaystyle \sum_{n=n_o}^\infty a_n\) converges, we can approximate the sum of the series \(S\) by one of its partial sums \(\displaystyle S_k=\sum_{n=n_o}^k a_n\). This approximation gets better as we include more terms. However, we need to have a bound on the error in the approximation.

If you approximate the convergent series \(\displaystyle S=\sum_{n=n_o}^\infty a_n\) by its \(k^\text{th}\) partial sum \(\displaystyle S_k=\sum_{n=n_o}^k a_n\), then the error in the approximation is \[\begin{aligned} E_k&=S-S_k \\ &=\sum_{n=n_o}^\infty a_n-\sum_{n=n_o}^k a_n =\sum_{n=k+1}^\infty a_n \end{aligned}\] which is the tail of the series beginning with the \((k+1)^\text{st}\) term.

Since the error is itself a series, any convergence test which provides a bound on the series can be used to bound the error in the approximation. These are the integral test and the comparison test. We start with the integral test.

1. Integral Bounds

Show that the series \(\displaystyle \sum_{n=1}^\infty \dfrac{1}{n^2}\) converges. Sum the first \(10\) terms to approximate the sum of the series. Find an upper bound on the error in the approximation.

We could say that \(\displaystyle \sum_{n=1}^\infty \dfrac{1}{n^2}\) converges because it is a \(p\)-series with \(p=2 \gt 1\). However, recall that the \(p\)-series are tested by using the integral test. So, in fact, \(\displaystyle \sum_{n=1}^\infty \dfrac{1}{n^2}\) converges because \(\dfrac{1}{n^2}\) is continuous, positive, decreasing and \[ \int_1^\infty \dfrac{1}{n^2}\,dn =\left[\dfrac{-1}{n}\right]_1^\infty =[0]-[-1]=1 \] is finite.

We approximate the sum of the series by the \(10^\text{th}\) partial sum \[\begin{aligned} \sum_{n=1}^\infty \dfrac{1}{n^2} &\approx S_{10}=\sum_{n=1}^{10} \dfrac{1}{n^2} \\ &=1+\dfrac{1}{4}+\dfrac{1}{9}+\dfrac{1}{16}+\dfrac{1}{25}+\dfrac{1}{36} +\dfrac{1}{49}+\dfrac{1}{64}+\dfrac{1}{81}+\dfrac{1}{100} \\ &\approx 1.5498 \end{aligned}\] The error in the approximation is \[ E_{10}=\sum_{n=1}^\infty \dfrac{1}{n^2}-\sum_{n=1}^{10} \dfrac{1}{n^2} =\sum_{n=11}^\infty \dfrac{1}{n^2} \] Since the terms \(\dfrac{1}{n^2}\) are positive, \(E_{10} \gt 0\). To put an upper bound on the error, we recall the Derivation of the Integral Test.

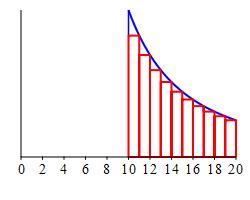
\[ E_{10}=\sum_{n=11}^\infty \dfrac{1}{n^2} \lt \int_{10}^\infty \dfrac{1}{n^2}\,dn =\left[\dfrac{-1}{n}\right]_{10}^\infty =[0] -\left[-\dfrac{1}{10}\right]=\dfrac{1}{10} \] Therefore, the error in the approximation \(\displaystyle \sum_{n=1}^\infty \dfrac{1}{n^2} \approx S_{10}=\sum_{n=1}^{10} \dfrac{1}{n^2} \approx1.5498\) is \(E_{10} \lt 0.1\).

To summarize (and generalize) this result, we have

Consider the series \(\displaystyle \sum_{n=1}^\infty \dfrac{1}{n^2+1}\).

1. Show that the series converges.
   

   The function \(\dfrac{1}{n^2+1}\) is continuous, positive, decreasing and \[ \int_1^\infty \dfrac{1}{n^2+1}\,dn =\left. \arctan n\right|_1^\infty =\dfrac{\pi}{2}-\dfrac{\pi}{4}=\dfrac{\pi}{4} \] which is finite. So \(\displaystyle \sum_{n=1}^\infty \dfrac{1}{n^2+1}\) converges by the integral test.

2. Approximate the sum of the series by summing \(100\) terms. Find the integral bound on the error in this approximation.

   \(\displaystyle S_{100}=\sum_{n=1}^{100} \dfrac{1}{n^2+1} \approx1.0667\) and \(E_{100}<.01\)

   The series may be approximated by the \(100^\text{th}\) partial sum: \[ S_{100}=\sum_{n=1}^{100} \dfrac{1}{n^2+1} \approx1.0667 \] (This should probably be done using some type of calculator.) The error in this approximation \(E_{100}\) is bounded by \[\begin{aligned} E_{100}&\lt \int_{100}^\infty \dfrac{1}{n^2+1}\,dn =\left.\arctan n\right|_{100}^\infty \\ &=\dfrac{\pi}{2}-\arctan100\approx .01 \end{aligned}\]

3. How many terms would you need to approximate the series to within \(10^{-6}\)?

   \(10^6\) terms

   If the series is approximated by the \(k^\text{th}\) partial sum \(\displaystyle S_k=\sum_{n=1}^k \dfrac{1}{n^2+1}\) then the error \(E_k\) is bounded by \[\int_k^\infty \dfrac{1}{n^2+1}\,dn=\left. \arctan n\right|_k^\infty =\dfrac{\pi}{2}-\arctan k\] We need to solve for \(k\) so that \(\dfrac{\pi}{2}-\arctan k=10^{-6}\). Thus \[ \arctan k=\dfrac{\pi}{2}-10^{-6} \] or \(k=\tan \left(\dfrac{\pi}{2}-10^{-6}\right) =\cot(10^{-6})=\dfrac{\cos(10^{-6})}{\sin(10^{-6})} \approx\dfrac{1}{10^{-6}}\approx10^6\) terms.

The answers for the above problems are useful, but the approximation to the series can be improved and the error estimate can be vastly reduced if we go one step further, as done on the next page. The problems on the subsequent pages use the Simple Comparison Test instead of the Integral Test.